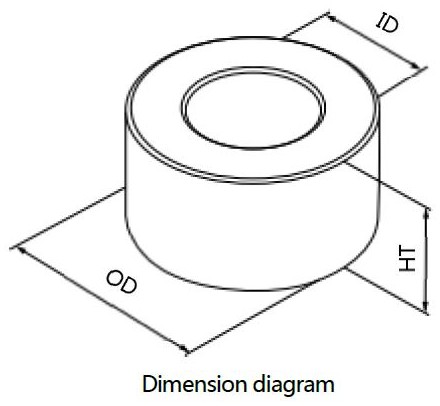
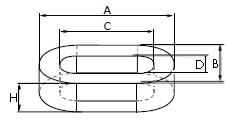
下記のような形状の磁気コアをトロイダルコアといい、多く使われるとともに、特性の計算も簡単にできます。回路設計上は、測定器で測定できるインダクタンス$L$(コイル巻数1のときは$A_L$)がわかれば充分ですが、コアの材料特性の比透磁率$\mu_e$(真空に対して、コアが入ったことによる効果)を知りたいことも多いです。
$$A_L \propto \mu_e$$
$$A_L = \frac{\mu_0 \cdot A_e}{l_e}\cdot \mu_e$$
この関係より、$A_L$と$\mu_e$は片方がわかれば、もう一方は簡単に計算できます。
例えば、外形 16*10*8 のサンプルの$L$を測定して、$A_L$ 29μHのとき、比透磁率 $\mu’$ は 約 39,300 とわかります。
トロイダルコアにコイルを巻数1とした時のインダクタンス$A_L$ と外形形状との関係は下記になります。
簡単のため巻数1として扱います。ナノ結晶材料の場合、比透磁率が10000以上あるので、実際のインダクタンス$L$測定の時も巻数1で十分測定できることが多いです。巻数1の時の$L$を$A_L$と表します。
$$A_L = \frac{\mu_0 \cdot \mu_e \cdot A_e}{l_e}$$
$A_e$: 断面積
$$A_e = \frac{(\text{OD} – \text{ID})}{2} \times H$$
$l_e$: 磁路長
$$l_e \approx \pi \times \frac{(\text{OD} + \text{ID})}{2}$$
$\mu_0$: 真空の透磁率
$\mu_e$: 比透磁率 真空のとき1として、磁性体が入ったことによる効果を表します。
この式をもとに、下記で求めます。
$$\mu_e = \frac{A_L \cdot l_e}{\mu_0 \cdot A_e}$$
$\mu=\mu’-j\mu”$ と考える時、実数部の$\mu’$の部分を対象に計算します。
透磁率 $$\mu’ = \mu_0 \cdot \frac{A_L}{L_0} 、L_0 = \frac{\mu_0 A_e}{l_e}$$
比透磁率 $$ (比透磁率) = \frac{\mu’}{\mu_0} = \frac{A_L}{L_0} = \frac{A_L \cdot l_e} {\mu_0 \cdot A_e}$$
外径 (OD): $16\,\text{mm}$内径 (ID): $10\,\text{mm}$高さ (H): $8\,\text{mm}$ 1Ts でのインダクタンスが29μH の μの算出
トロイダルコアの「実効磁路長($l_e$)」と「実効断面積($A_e$)」の計算。
① 実効断面積 ($A_e$) : 断面積は長方形として計算します。
$$A_e = \frac{(\text{OD} – \text{ID})}{2} \times H$$
$$A_e = \frac{(16 – 10)}{2} \times 8 = 3 \times 8 = 24\,\text{mm}^2 = 24 \times 10^{-6}\,\text{m}^2$$
② 実効磁路長 ($l_e$) : 一般的に平均径を用いて近似します。
$$l_e \approx \pi \times \frac{(\text{OD} + \text{ID})}{2}$$
$$l_e \approx \pi \times \frac{26}{2} = 13\pi \approx 40.84\,\text{mm} = 0.04084\,\text{m}$$
$A_L$ 値(インダクタンス係数)の定義式から逆算します。
一般的に $A_L$ は「1ターンあたりのインダクタンス」として定義され、単位が $[\text{H}/\text{N}^2]$ の場合、式は以下のようになります。
$$A_L = \frac{\mu_0 \cdot \mu_e \cdot A_e}{l_e}$$
これを $\mu_e$(比透磁率)について解きます。
$$\mu_e = \frac{A_L \cdot l_e}{\mu_0 \cdot A_e}$$
数値を代入します。
$$\mu_e = \frac{(29 \times 10^{-6}) \times 0.04084}{(4\pi \times 10^{-7}) \times (24 \times 10^{-6})}$$
$$\mu_e = \frac{1.18436 \times 10^{-6}}{30.159 \times 10^{-12}}$$
$$\mu_e \approx 39,270$$
計算結果より、外形 16*10*8 で $A_L$ 29μHのとき、比透磁率 $\mu_e$ は 約 39,300 。